Selection Sort in C, C++, Python, Java, Php

---

C Implementation Of Selection Sort    , C++ Implementation Of Selection Sort    , Python Implementation Of Selection Sort    , Java Implementation Of Selection Sort    , PHP Implementation Of Selection Sort

---

Selection sort

In sectional sort if there are “n” elements then
in first pass we search through the table and find the smallest element, when found we interchange with the element at the first position.
In the second pass we locate the second lowest element and when found we interchange with the element at the second position. And so on.
As each pass places one record at its proper place, so we need total of n-1 passes to perform the sort.

Example:

Elements: 8, 20, 2, 1, 4, 19, 7, 12

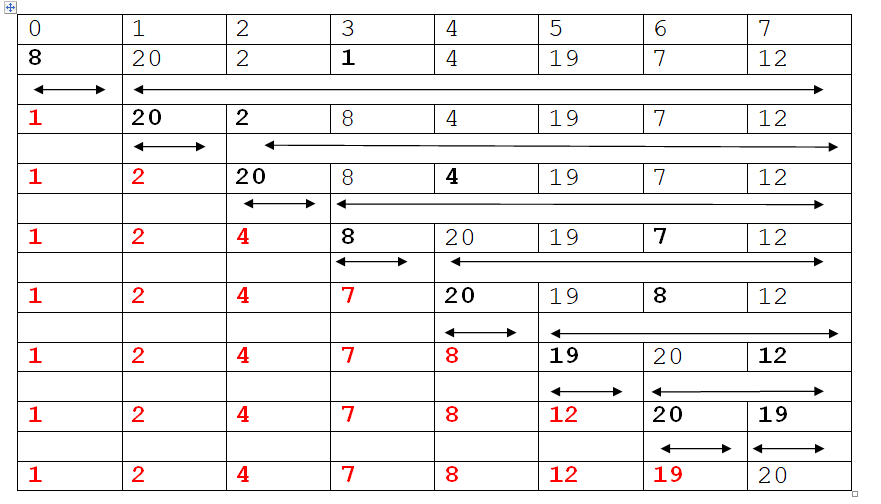
Note: After this step list automatically gets sorted (not required to check for the last element) so n-1 passes are required.

Advantages:

* Easy to implement.
* Requires no additional storage space.
* It performs well on a small list.

Disadvantages:

* Poor efficiency when dealing with a huge list of items.
* Its performance is easily influenced by the initial ordering of the items before the sorting process.
* It lacks efficiency on huge list of items.
* It does not stop unless the number of iterations has been achieved even though the list is already sorted.

Complexity

Time complexity of a selection sort is calculated in terms of the number of comparisons. There are two loops one nested with in the other. During the 1st pass n-1 comparisons are made. In the 2nd pass n-2 comparisons are made. In general in ith pass n-i comparisons are made. Thus the total numbers of comparisons are
(n-1) + (n-2) + . . . . +3 + 2 + 1
N*(n-1)/2

Therefore, the number of comparisons for the selection sort is proportional to n2, which means it is order of n2 i.e. O(n2).

Worst case: In worst case we can analyze how the algorithm is performed for reverse sorted arrat as input.

Average case : In average case where we input general (mixed sorted) input to the algorithm.

Following table will summaries the efficiency of algorithm in different cases.

Best Case	Worst Case	Average Case
(n-1)=O(n)	N(n-1)/2=O(n2)(n square)	N(n-1)/2=O(n2)(n square)
Order of n	Order of n square	Order of n square

C Selection Sort

C Implementation Of Selection Sort

/* selection sort */
#include<stdio.h>
#include<conio.h>
void main()
{
int a[30],i,j,t,n,min,pos;
clrscr();
printf("enter the total number of elements ");
scanf("%d",&n);
printf("enter the node elements \n");
for(i=0;i<=n-1;i++)
{
printf("enter the %d element ",i+1);
scanf("%d",&a[i]);
}
/* to sort */
for(i=0;i<n-1;i++)
{
min=a[i];
pos=i;
for(j=i+1;j<n;j++)
{
if (min>a[j])// if(a[j]<min)
{
min=a[j];
pos=j;
}
}
t=a[i];
a[i]=a[pos];
a[pos]=t;
}
printf("sorted elements list is \n");
for(i=0;i<=n-1;i++)
{
printf("%d\n",a[i]);
}
getch();
}

C++ Selection Sort

C++ Implementation Of Selection Sort

/* selection  sort*/
 #include<iostream.h>
 #include<conio.h>
 void selection(int [],int);
  
 void main()
 {
 int a[30],i,n;
 clrscr();
 cout<<"enter the total number of elements ";
 cin>>n;
 cout<<"enter the node elements \n";
 for(i=0;i<n;i++)
 {
 cout<<"enter the  element ";
 cin>>a[i];
 }
 selection(a,n);
 cout<<"sorted elements list is \n";
 for(i=0;i<n;i++)
 {
 cout<<a[i]<<endl;
 }
 getch();
 }
 void selection(int a[],int n)
 {
 int i,j,min,t,pos;
 for(i=0;i<n-1;i++)
 {
 min=a[i];
 pos=i;
 for(j=i+1;j<n;j++)
 {
 if (a[j]<min)
 {
 min=a[j];
 pos=j;
 }
 }
 t=a[i];
 a[i]=a[pos];
 a[pos]=t;
 }
 } 

Python Selection Sort

Python Implementation Of Selection Sort

def selection_sort(n):
     for i in range(0, len(n) - 1):
         smallest = i
         for j in range(i + 1, len(n)):
             if(n[j] < n[smallest]):
                 smallest = j
         n[i], n[smallest] = n[smallest], n[i]
 n = input('Enter the list of numbers: ').split()
 n = [int(x) for x in n]
 selection_sort(n)
 print('Sorted list: ', end='')
 print(n)

Output:

Enter the list of numbers: 5 3 26 9 7 5 2 3
Sorted list: [2, 3, 3, 5, 5, 7, 9, 26]
>>>

Tutorials	Technical Questions	Interview Questions
C Programming C++ Programming Class 11 (Python) Class 12 (Python)	C Language C++ Programming Python	C Interview Questions C++ Interview Questions C Programs C++ Programs